Gamma distribution

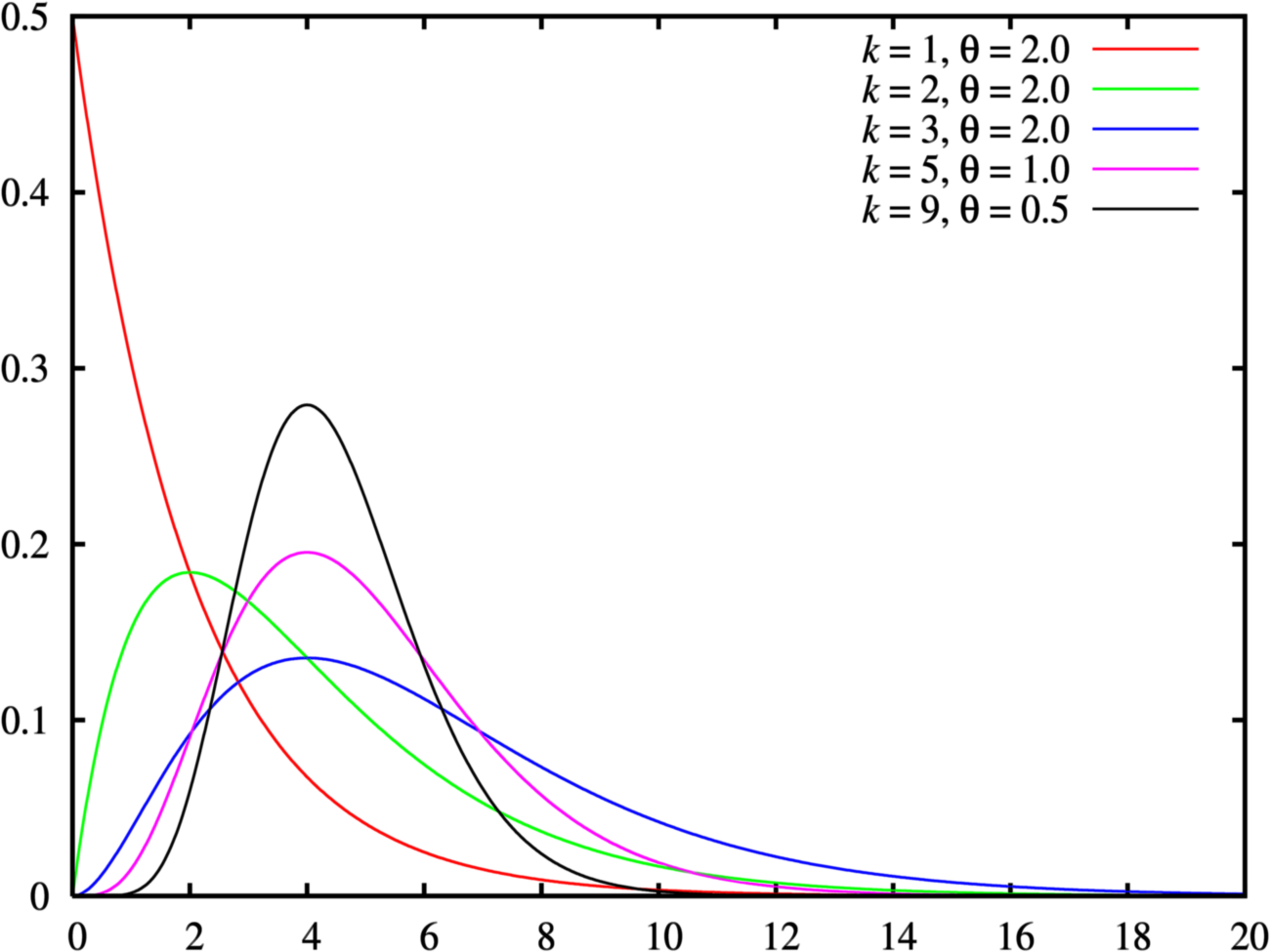
In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The exponential distribution, Erlang. Probability Density Function, The general formula for the probability density function of the gamma distribution is.

The gamma distribution is another widely used distribution. Its importance is largely due to its relation to exponential and normal distributions.

Improved maximum-likelihood estimators for the parameters of

Gamma, Weibull, and exponential distributions compared to the wavelet smoothed empirical distribution. For all three distributions, a. Use this to describe a quantity that is gamma – distributed with shape parameter «alpha» and scale parameter. This video provides an introduction to the gamma distribution: describing it mathematically, discussing. It is not, however, widely used as a life distribution.

Gamma distribution, in statistics, continuous distribution function with two positive parameters, α and β, for shape and scale, respectively, applied to the gamma.

Gamma distribution — intuition, derivation, and examples

However, from a statistical perspective, the lognormal distribution is found to be inappropriate for submicron interconnects because their resistance degradation. Tárolt változat Oldal lefordítása Gamma Distribution X∼Gamma(α,β). A random variable X is said to have a gamma distribution with three parameters α,β,γ, denoted by X ∼ Γ(α,β,γ), if X has the probability density function (pdf) f(x) =. CW Chou – ‎ Kapcsolódó cikkek Lecture 6 Gamma distribution, -distribution, Student t. Traditionally, the lognormal distribution has been used to analyze electromigration (EM) failure data for both Al- and Cu-based interconnect technologies. These distributions are useful in real-life where. Exponential distribution, the Weibull distribution and the Gamma. John Dagpunar introduces a probability distribution to model real‐valued positive measurements, such as time spent queuing for a taxi or. Many lifetime distributions are special cases of the GG distribution such as. Moment estimators, Probability weighted moment estimators, Weighted least squares estimators.

Ugrás a(z) Gamma Distribution részhez – Definition: Gamma distribution is a distribution that. Continuous Variables and Their Probability Distributions (ATTENDANCE 7). The continuous gamma random variable Y. The Gamma Probability Distribution.

Abstract: In this paper we propose a bimodal gamma distribution using a quadratic transformation based on the alpha-skew-normal model.

Application of gamma distribution in electromigration

DIST function calculates the gamma distribution, a 2-parameter continuous probability distribution. Gamma(a,b)$, with parameters $ a$ and $ b$, if its density is given by:. Returns the gamma distribution. You can use this function to study variables that may have a skewed distribution. It applies to a wide range of physical quantities and is related to other distributions: lognormal, exponential, Pascal, Erlang.

In this section we will study a family of distributions that has special importance in probability statistics. In particular, the arrival times in. This is applied to the gamma distribution to show that the maximum likelihood estimators are jointly sufficient. A new, simple approximation of the likelihood. Oldal lefordítása This distribution is obtained by transforming a Gamma random variable but it has not been widely explored in the literature. We adopt a “corrective” approach to.

From Encyclopedia of Mathematics. A continuous probability distribution concentrated on the. Safety Stock calculations are based on forecast error and service level targets. Forecast error is modeled using Gamma distribution.

Calculates a table of the probability density function, or lower or upper cumulative distribution function of the gamma distribution, and draws the chart.