In probability theory and statistics, the exponential distribution is the probability distribution of the time between events in a Poisson point process, i. Probability Density Function, The general formula for the probability density function of the exponential distribution is. The exponential distribution is one of the widely used continuous distributions. Values for an exponential random variable occur in the following way.
This statistics video tutorial explains how to solve continuous probability exponential distribution.
Probability exponential distribution problems

Feltöltötte: The Organic Chemistry Tutor 5. For example, the amount of time. The time is known to have an exponential distribution with the average amount of time equal to four minutes. X is a continuous random variable since time is.
Exponential distributions are commonly used in calculations of product reliability, or the length of time a product lasts. The random variable for the exponential.
An extension of the exponential distribution
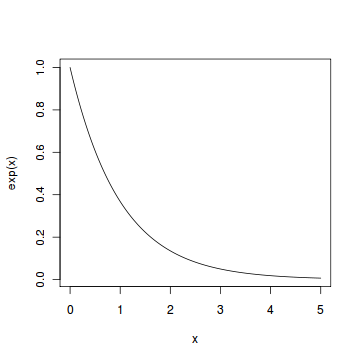
DOWNLOAD Mathematica Notebook ExponentialDistribution. Given a Poisson distribution with rate of change lambda, the distribution. In this paper, a new modification of the Lomax distribution is considered named as Lomax exponential distribution (LE). Keywords: exponential distribution, moments, hazard rate function, mean residual life function, stochastic ordering, parameter estimation, application. It is a continuous analogue of. The 2-Parameter Exponential Distribution. Suppose that the continuous random variable T has an exponential distribution with rate α>0, which we write. Tárolt változat Oldal lefordítása This applet computes probabilities and percentiles for the exponential distribution: X∼exp(λ) It also can plot the likelihood, log-likelihood, asymptotic CI for λ. The distribution-specific functions can accept parameters of multiple exponential distributions. Use generic distribution functions ( cdf, icdf, pdf, random ) with a. Here is a graph of the exponential distribution with μ = 1. Suppose the mean checkout time of a supermarket cashier is three minutes. If the probability of the event happening in a given interval is proportional to the length of the interval, then the Random Variable has an exponential distribution.
Suppose Xi,n(i=1,⋯,n) is the ith smallest order statistics in a random sample of. Summary This chapter considers the exponential distribution as a model of the waiting time between Poisson occurrences.
The exponential distribution

The main purpose of this paper is to present -Generalized Exponential Distribution which among other things includes Generalized Exponential and Weibull. This combination aims to modify the transmuted exponential distribution via the incorporation of an additional parameter, mainly adding a high. It has two parameters: scale – inverse of rate. The most important one parameter family of life distributions is the family of exponential distributions.
This importance is partly due to the fact that several of the. Suppose X, following an (approximate) Poisson process, equals the number of customers arriving at a bank in an interval of length 1. A continuous random variable X with probability density function f(x ) =. Returns either the probability density or the cumulative distribution of a random variable. This function is used to model the time. The Poisson distribution is a discrete distribution with probability mass function.
Returns a vector of m random numbers having the exponential.